Question

12 workers can do a piece of work in 30 days. Find how many workers should be added to finish the work in 24 hours. ​

Answer 1

Workers to be be added to finish the work in 24 hours = 348

Explanation:

This is a problem involving inverse proportion

Here the number of days required to complete the job is inversely proportional to the number of workers- the more the workers, the less time it takes

We can state this as:

`D \propto (1)/(N)`

where D = time in days required to complete the job and N is the number of workers that can do this in D days

The equation relating D and N can be stated as

`D = k (1)/(N)`

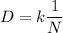
This gives us k = D x N (multiply by N both sides)

where k is a constant known as the constant of proportionality

Given data that D = 30 when N = 12, this constant of proportionality = D x N = 30 x 12 = 360

From the equation of proportionality we also get
N = k/D

So to complete the job in 24 hours = 1 day, substitute 1 for D and 360 for k to get
N = 360/1 = 360 workers

So you will need 360-12 = 348 workers if you expect to finish the job in 24 hours = 1 day