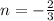Answer:
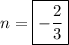
Explanation:
![\frac{1}{( {\sqrt[3]{5}})^(2) } = {5}^(n) \\](https://img.qammunity.org/2023/formulas/mathematics/college/z55unupah4ce0ppyc7dt8948qi35pfnkqx.png)
- Change or convert the cube root into an index form; ³√x = x^⅓
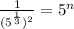
- Open the brackets by multiplying the powers; (a²)² = a²×²
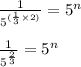
- Following the law of indices below;
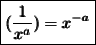
- Therefore;
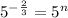
- Since the bases (5) are the same, the powers are equal;