Answer:
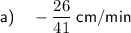
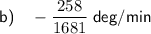
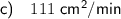
Explanation:
Define the variables:
- Let x = width of the rectangle
- Let y = length of the rectangle
Given that the width of the rectangle is decreasing at a rate of 2 cm/min:
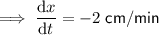
Given that the length of the rectangle is increasing at a rate of 6 cm/min:
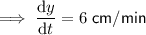
Part (a)
The diagonal forms a right triangle.
Therefore, using Pythagoras Theorem:
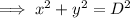
where D is the length of the diagonal.
To find the rate of change of the diagonal, take the derivative of the equation with respect to time (t):
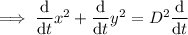
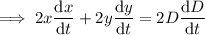
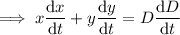
Given:
Use Pythagoras Theorem to calculate the width of the rectangle:
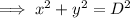
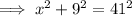
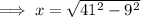
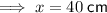
Given parameters:
Substitute the given parameters into the equation:
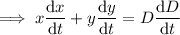
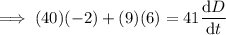
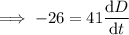
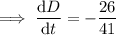
Therefore, the length of the diagonal is decreasing at a rate of ²⁶/₄₁ cm/min.
Part (b)
Note: The angle θ has not been marked on the given diagram.
Therefore, I have used the angle BAC (please see attached diagram).
If θ is the angle BAC then to find the rate of change of the angle, find an expression for the angle using the tan ratio:
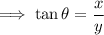
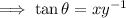
To find the rate of change of the angle, take the derivative of the equation with respect to time (t):
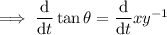
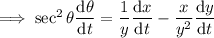
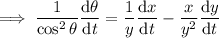
Given:
- x = 40 cm
- y = 9 cm
- D = 41 cm
Find an expression for the cosine of angle θ using the given parameters:
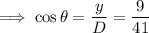
Given parameters:
Substitute the given parameters into the equation:
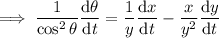
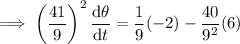
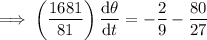
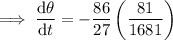
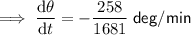
Therefore, the angle is decreasing at a rate of ²⁵⁶/₁₆₈₁ deg/min.
Part (c)
The equation for the area of triangle ABC is:
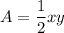
To find the rate of change of the area, take the derivative of the equation with respect to time (t):
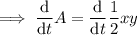
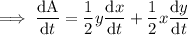
Given parameters:
Substitute the given parameters into the equation:
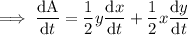
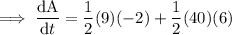
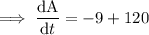
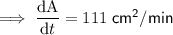
Therefore, the area of the triangle is increasing at a rate of 111 cm²/min.