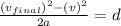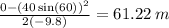Step-by-step explanation:
The maximum height of the projectile occurs when the velocity in the vertical direction is 0.
we know
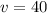
and that
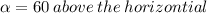
Since we have a magnitude vector and an direction angle, we need to break this vector up into components.
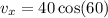
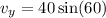
Next, we know g is

and our
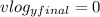
We know to find d, the vertical height.
Using our kinematic equations, we can use
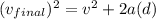
Since we referring to the y direction, our subscripts will be y.
First, isolate the quantity, d, and plug in knowns