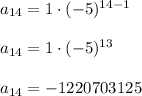Question

Find the 14th term of the geometric sequence 1, -5, 25,

Answer 1

-1220703125

Explanation:

The formula for the nth term of a geometric sequence is given by

`a_n = a_1\cdot r^(n-1)`

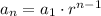
where

`a_n = \text{ nth term}\\\\a_1 = \text{first term}\\\\r = \text{common ratio} = (a_n)/(a_1)\\`
The common ratio is found by dividing any term in the sequence by the preceding term

In the sequence 1, -5, 25,

first term a₁ = 1
common ratio r = -5/1 = 25/-5 = -5

So nth term is given by

`a_n = 1 \cdot (-5)^(n-1)`

14th term is

`a_(14) = 1 \cdot (-5)^(14-1)\\\\a_(14) = 1 \cdot (-5)^(13)\\\\a_(14) = -1220703125`