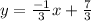Answer:
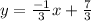
Explanation:
Hey! Let's help you with your question here!
So here, we're already given your slope which is wonderful! That is less work to figure out. Now we have to put all of this together into slope-intercept form. To recall, the slope-intercept form is:

We have our m, which is our slope
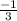 and we have a point that's on the line (-2, 3). We can actually figure out the equation with all of this information!
and we have a point that's on the line (-2, 3). We can actually figure out the equation with all of this information!
All we need to do is to sub in the slope as m and then substitute the point that we have into x and y respectively, so it becomes:
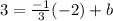
Now, all we have to do is solve for b:
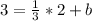 - Cancelling out the negatives.
- Cancelling out the negatives.
 - Making the 2 into a fraction for easy multiplication.
- Making the 2 into a fraction for easy multiplication.

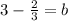 - Moving all the values to the other side to solve for b.
- Moving all the values to the other side to solve for b.
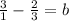 - Making the 3 into a fraction for easy subtraction.
- Making the 3 into a fraction for easy subtraction.
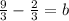 - Multiplied the first fraction by 3 to get least common denom
- Multiplied the first fraction by 3 to get least common denom

Therefore, the formula that can be made from this is: