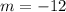Answer:
(2, 1) and (4, 2):

(-4, 5) and (-3, -7):
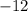
Explanation:
Hello! Let's help you with that problem there!
So we know that in a slope intercept form, it is depicted as
 . There are two ways to essentially find m, which is slope in this case. The first method is the
. There are two ways to essentially find m, which is slope in this case. The first method is the
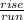 method. This is typically used when you have a graph to look off from and it's just a matter of counting the displacement from one point to another.
method. This is typically used when you have a graph to look off from and it's just a matter of counting the displacement from one point to another.
However, there is another way to find the slope given 2 points and that is what we are going to do here, since we have no graph to reference and have all the relevant information to find the slope using this formula:

With this formula, we can plug in the coordinate values and solve for the slope!
(2, 1) and (4, 2):
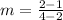
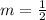
Therefore, the slope of these points is
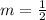
(-4, 5) and (-3, -7):
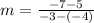
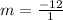
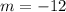
Therefore, the slope of these points is
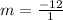 or
or