Answer:
(Assumption: air resistance on the rock is negligible;
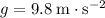 .)
.)
The rock travelled
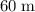 horizontally.
horizontally.
The cliff is approximately
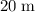 above the water.
above the water.
The overall displacement of the rock is approximately
 .
.
Horizontal velocity of the rock right before it hit the water:
 (same as when the rock was launched.)
(same as when the rock was launched.)
Vertical velocity of the rock right before it hit the water: approximately
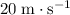 .
.
Step-by-step explanation:
Assume that the air resistance on the rock is negligible. During the entire flight, the horizontal velocity of the rock will be constantly
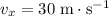 . The vertical velocity of the rock will uniformly increase at a rate of
. The vertical velocity of the rock will uniformly increase at a rate of
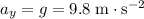 (this rate is the vertical acceleration of the rock.)
(this rate is the vertical acceleration of the rock.)
Since the horizontal velocity of the rock is constant, multiply that velocity by time to find the horizontal displacement:
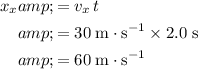 .
.
Let
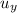 denote the initial vertical velocity of the rock. In this question,
denote the initial vertical velocity of the rock. In this question,
 since the stone was thrown horizontally.
since the stone was thrown horizontally.
While the vertical velocity of the rock isn't constant, vertical acceleration
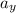 is constant. Hence, apply the SUVAT equation
is constant. Hence, apply the SUVAT equation
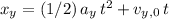 to find the vertical displacement
to find the vertical displacement
 :
:
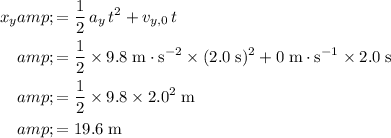 .
.
The height of the cliff (relative to the water underneath) is equal to the vertical displacement of the rock:
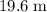 (approximately
(approximately
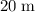 when rounded to two significant figures.)
when rounded to two significant figures.)
The horizontal and vertical displacement of this rock are perpendicular to one another. These two displacements
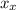 and
and
 form the two sides of a right triangle, with the overall displacement
form the two sides of a right triangle, with the overall displacement
 as the other side (the hypotenuse.) The overall displacement of this rock can be found using the Pythagorean Theorem:
as the other side (the hypotenuse.) The overall displacement of this rock can be found using the Pythagorean Theorem:
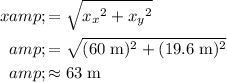 .
.
Again, assume that air resistance on the rock is negligible. The horizontal velocity of the rock right before hitting the water will be the same as the initial value:
 .
.
Let
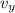 denote the vertical velocity of the rock right before hitting the water. Apply the SUVAT equation
denote the vertical velocity of the rock right before hitting the water. Apply the SUVAT equation
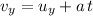 to find
to find
 :
:
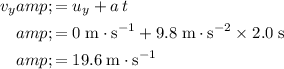 .
.
Hence, right before hitting the water, the vertical velocity of this rock will be
 (rounded to
(rounded to
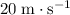 .)
.)