Question

Write a quadratic function f whose zeros are -3 and -10.

Answer 1

`f(x)=x^(2) +13x+30`

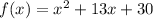
Explanation:

1. Whenever you write a quadratic function with zeros, you want to put it into a formula like this:

`f(x)= (x-p) (x-q)`

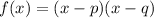
p and q are the zeros

2. Your zeros are (-3) and (-10). When plugging in the zeros, you always flip the sign on the number. Because you would plug it in as:
`f(x) = (x-(-3)) (x-(-10))`

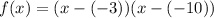
Two negative signs equal positive signs, so the equation will look like this:

`f(x)=(x+3)(x+10)`

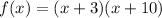
3. Solve the equation:

a. Use the foil method:
`(a+b)(c+d)=ac+ad+bc+bd`

`f(x)=x^(2) +10x+3x+30`

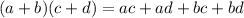
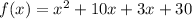
b. Collect like terms

`f(x)=x^(2) +(10x+3x)+30`

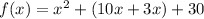
c. Simplify

`f(x)=x^(2) +13x+30`

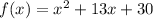
Hope that helps!