Question

Can someone help me with part A on this question? I'm stuck on it :(

Answer 1

Discriminant: b² - 4ac < 0

The equation has no real solution; two imaginary solutions.

Explanation:

The discriminant, b² - 4ac is the expression under the radical of the quadratic formula,
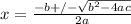`x = \frac{-b +/- \sqrt{b^(2)-4ac} }{2a}`. Knowing the value of a quadratic equation's discriminant allows us to determine its nature (real or complex) and its number of solutions, if any.

The following values of discriminant define the nature and number of solutions:

b² - 4ac = 0 ⇒ The equation has one real solution or root. This means that the graph will cross the x-axis once.

b² - 4ac > 0 ⇒ The equation has two real solutions or roots. This means that the graph will cross the x-axis twice.

b² - 4ac < 0 ⇒ The equation has no real solution or have two imaginary roots. This means that the graph will not cross the x-axis at all.

Provided these definitions, it is easier to determine the possible discriminant for your given graph: b² - 4ac < 0 since the parabola doesn't cross the x-axis at all. This implies that the quadratic equation doesn't have any x-intercepts.

Therefore, the given graph of a quadratic equation does not have any real solution (no solution). Instead, it will have two imaginary or complex solutions or roots.