Answer:
$28 on 2 hours of additional charges.
Explanation:
Hello! Let's help you with your question here!
To begin, let's start writing these in terms of system of equations. Given your parameters we can split it up!
River Rafting Company A:
Here, we have a $18 cost for rental and an additional charge of $5 each hour. The $18 cost is essentially our flat rate, we have to pay this regardless and it's a one-time payment. The $5 each hour is our variable cost as we are unsure of how long people are going to be renting them for. So we can write the equation as:
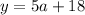
River Rafting Company B:
Over on this side, we have a $22 cost for rental and an additional charge of $3 each hour. The explanation is the exact same as the previous one. We have a higher flat rate of $22 but a lower variable cost of $3 each hour. Therefore, the equation is:
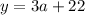
Now that we have equations for both companies, we can solve using systems of equations to get y, since we are trying to get the total cost of both companies to be same. For this, let's solve with substitution.
Solve by Substitution:
Okay! Let's take
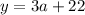 (Equation 1) and substitute it into
(Equation 1) and substitute it into
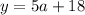 (Equation 2). To do this, we just essentially have substitute y in Equation 2 with the values that it equals to in Equation 1, so it becomes:
(Equation 2). To do this, we just essentially have substitute y in Equation 2 with the values that it equals to in Equation 1, so it becomes:
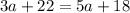
Now, we solve for a, we move everything over to one side and then collect like terms. For this, I will be moving everything to the right. So it becomes as follows:
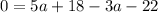

From here, we divide x and -4 by 2 to isolate a. We finally get
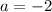 . Time cannot be negative which means it has to be
. Time cannot be negative which means it has to be
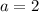 instead.
instead.
Now that we finally have the value of a, we can use that value and substitute it into Equation 1 to get the total cost y. So that would be:
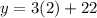
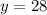
Let's try this for the second equation to verify that the cost are the same:
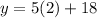
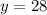
Here, both y values are equal to 28. Therefore, you use solve by substitution to figure out that the total cost for both equals $28 when under the additional charge of 2 hours.