(a) Recall the definition of the step function,
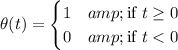
Then we have
•
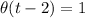 if
if
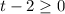 , or
, or
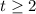
•
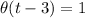 if
if
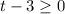 , or
, or
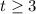
and we can combine these to get
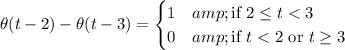
then scale up by 4 to get the value we want over [2, 3].
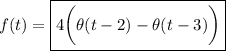
At least that's what I get using the aforementioned definition of "step function". I don't see a way to have both
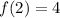 and
and
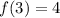 with this definition...
with this definition...
(b) No function was given...