Question

MATRECIES: Suppose ={u,v,w}⊆R3 is linearly independent. Determine if the set 4 ={u, v, v−w, u+v+w} is linearly independent or linearly dependent.

Answer 1

The set is linearly dependent.

To explicitly prove this, we need to show there is at least one choice of constants
`c_1,c_2,c_3,c_3\in\Bbb R` such that

`c_1 u + c_2 v + c_3(v-w) + c_4(u+v+w) = 0`

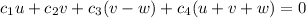
or equivalently,

`(c_1 + c_4) u + (c_2 + c_3 + c_4) v + (-c_3 + c_4) w = 0`

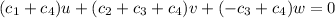
which is the same as solving the system of equations

`\begin{cases} c_1 + c_4 = 0 \\ c_2 + c_3 + c_4 = 0 \\ -c_3 + c_4 = 0 \end{cases}`

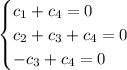
From the first and last equations, we have
`c_1=-c_4` and
`c_3=c_4`. Substituting these into the second equation leaves us with
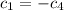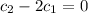`c_2-2c_1=0`, and so the overall solution set is

`c_1 = \frac12 c_2 = -c_3 = -c_4`

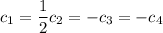
for which there are infinitely many not-all-zero solutions.