Question

while playing lawn darts with his friend, jack notices that when he throws a dart up at 60 degrees it travels 11 meters. how high did the dart travel?

Answer 1

Answer: Approximately 9.526279 meters

======================================================

Step-by-step explanation:

See the diagram below.

Draw a horizontal line to mark points A, B and C on it

A = dartboard

B = Jack's location

C = midpoint of A and B

Segment AB is the 11 meter horizontal distance from Jack to the dartboard. Half of this is BC = 11/2 = 5.5 meters.

Then just above point C, we'll have a fourth point D. Segment CD is the unknown max height of the dart. Let's call this x.

The dart will begin at point B, go upward in a parabolic arc to get to point D (the peak of the mountain), then come back down to arrive at point A.

------------------------------------

Focus on triangle BCD. Angle B = 60 degrees is the angle of elevation that Jack uses to throw the dart.

We'll use the tangent ratio to connect the opposite side x to the adjacent side 5.5

`\tan(\text{angle}) = \frac{\text{opposite}}{\text{adjacent}}\\\\\tan(\text{B}) = \frac{\text{CD}}{\text{BC}}\\\\\tan(60) = \frac{\text{x}}{5.5}\\\\\text{x} = 5.5*\tan(60)\\\\\text{x} \approx 9.526279\\\\`

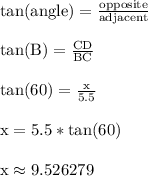
Make sure your calculator is in degree mode.

Segment CD is approximately 9.526279 meters which is the max height the dart reaches.

See the diagram below.