Question

Please help will give 50points

Answer 1

a=10

Explanation:

Using Pythagoras theorem

`{(a + 2)}^(2) + {( a- 5)}^(2) = {(a + 3)}^(2)`

`{a}^(2) + 4a + 4 + {a}^(2) - 10a + 25 = {a}^(2) + 6a + 9`

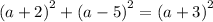
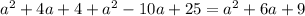
simplify:

`{a}^(2) - 12a + 20 = 0`

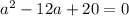
(a-2)(a-10)=0

hence a= 2 or a=10 however we must reject 2 as the lengths of the triangle cannot be negative eg. the side for a-5 will be equivalent to -3 cm which is not possible for lengths to become negative