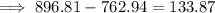Question

100 POINTS PLEASE HELP

Lisa is saving for college. The account is modeled by the function: F (x) = 250(1.25)^x , when x represents how many years she has saved.

Xavier is also saving for college. His account is modeled by this table:

x 0 1 2 3
g(x) 200 270 364.5 492.08
Answer the following questions:

A. After 5 years, how much does Lisa's account have in it?

B. After 5 years, how much does Xaviers account have in it?

C. What is the positive difference in their accounts after 5 years?

Show your work. (this does not have to be done by hand, but just show what you would enter into the calculator)

Answer 1

A. $762.94

B. $896.81

C. $133.87

Explanation:

Given function modelling Lisa's saving account:

`\boxed{f(x)=250(1.25)^x}`

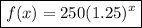
where x is the number of years.

Given table modelling Xavier's savings account:

`\begin{array}c\cline{1-5} x & 0 & 1 & 2 & 3\\\cline{1-5} g(x) & 200 & 270 & 364.5 & 492.08\\\cline{1-5}\end{array}`

Part A

To find the amount in Lisa's savings account after 5 years, substitute x=5 into the function:

`\begin{aligned}\implies f(5)&=250(1.25)^5\\&=250(3.051757...)\\&=762.939453...\end{aligned}`

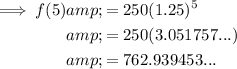
Therefore, the amount in Lisa's savings account after 5 years is $762.94 (nearest cent).

Part B

First, create an exponential function to model Xavier's savings account.

General form of an exponential function:

`y=ab^x`

where:

• a is the initial value (y-intercept).
• b is the base (growth/decay factor) in decimal form.

From inspection of the given table, the initial value (a) is 200.

`\implies g(x)=200b^x`

To find the value of b, substitute point (1, 270) into the function:

`\begin{aligned}\implies g(1)=200b&=270\\b&=(270)/(200)\\b&=1.35\end{aligned}`

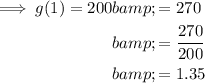
Therefore. the function that models Xavier's savings account is:

`\boxed{g(x)=200(1.35)^x}`

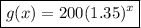
To find the amount in Xavier's savings account after 5 years, substitute x=5 into the found function:

`\begin{aligned}\implies g(5)&=200(1.35)^5\\&=200(4.4840334...)\\&=896.806687...\end{aligned}`

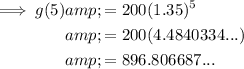
Therefore, the amount in Xavier's savings account after 5 years is $896.81 (nearest cent).

Part C

To find the positive difference in their accounts after 5 years, subtract Lisa's balance from Xavier's balance:

`\implies 896.81-762.94 =133.87`