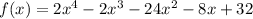Answer:

Explanation:
The zeros of a function are the x-values of the points at which the curve intersects the x-axis.
From inspection of the given graph, the polynomial has zeros at:
- x = -2 with multiplicity 2 (as the curve touches the x-axis).
- x = 1
- x = 4
The end behaviour of the function is:
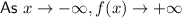
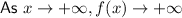
This means that:
- The degree of the function is even.
- The leading coefficient is positive.
Therefore:

Substitute the given point (-1, 20) into the function and solve for a:
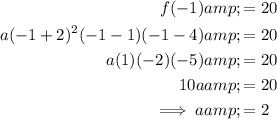
Therefore, the formula for the function is:
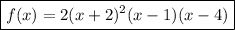
In standard form: