Answer:
Jos is 14 years
Explanation:
Let Father's age be x
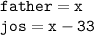
- The question says, product of their ages is 658
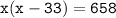
- Open the brackets following distributive property;
-
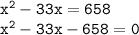
- Using bulldozer method;
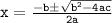
- A general quadratic equation has a format ax² + bx + c = 0

- Father's age = 47 years
- Jos's age = (47 - 33) = 14 years