Question

1/3log(1-x)=log(x+1)+1/3

Answer 1

`x = -0.472 \; \sf (3\;d.p.)`

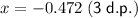
Explanation:

Given equation:

`(1)/(3) \log(1-x)=\log(x+1)+(1)/(3)`

`\textsf{Apply the log power law}: \quad n\log_ax=\log_ax^n`

`\implies \log(1-x)^{(1)/(3)}=\log(x+1)+(1)/(3)`

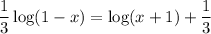
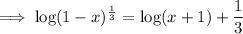
Subtract log(x + 1) from both sides:

`\implies \log(1-x)^{(1)/(3)}-\log(x+1)=(1)/(3)`

`\textsf{Apply the log quotient law}: \quad \log_ax - \log_ay=\log_a \left((x)/(y)\right)`

`\implies \log \left(\frac{(1-x)^{(1)/(3)}}{x+1}\right)=(1)/(3)`

`\textsf{Apply the log law}: \quad \log_ab=c \iff a^c=b`

`\implies 10^{(1)/(3)}=\frac{(1-x)^{(1)/(3)}}{x+1}`

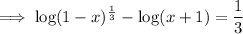
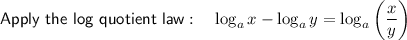
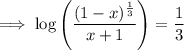
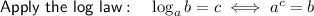
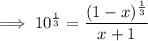
`\textsf{Apply the exponent rule}: \quad a^{(1)/(n)}=\sqrt[n]{a}`

`\implies \sqrt[3]{10} =\frac{\sqrt[3]{1-x}}{x+1}`

Multiply both sides by (x + 1):

`\implies \sqrt[3]{10}(x+1)=\sqrt[3]{1-x}}`

Cube both sides:

`\implies 10(x+1)^3=1-x`

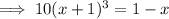
Expand the left side:

`\implies 10(x+1)(x+1)(x+1)=1-x`

`\implies 10(x+1)(x^2+2x+1)=1-x`

`\implies 10(x^3+3x^2+3x+1)=1-x`

`\implies 10x^3+30x^2+30x+10=1-x`

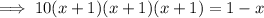
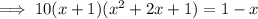
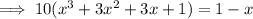
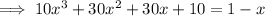
Subtract 1 and add x to both sides:

`\implies 10x^3+30x^2+31x+9=0`

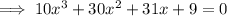
Find the roots of the cubic function by graphing, using a calculator, or by a numerical method.

Real root:

`x = -0.472 \; \sf (3\;d.p.)`

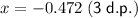
Complex roots:

`x=(-1.264 + 0.556i)\; \sf (3\;d.p.)`

`x=(-1.264 - 0.556i)\; \sf (3\;d.p.)`

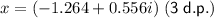
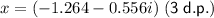
Therefore, the only valid solution is the real root:

`x = -0.472 \; \sf (3\;d.p.)`

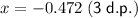
As we can only take logs of positive numbers, substitute the real root into (1 - x) and (x + 1) to check:

`x=-0.472 \implies 1-(-0.472)=1.472 > 0`

`x=-0.472 \implies -0.472+1=0.528 > 0`

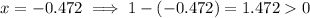
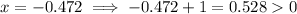
As both results are positive, this is a valid solution for the given equation.

(Proof of the solution is in the attached graph).