Question

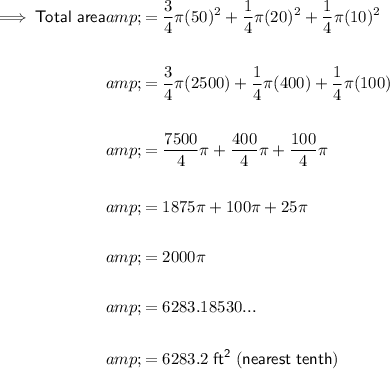
my rectangular house is 30 feet by 40 feet. My goat Cassidy is outside on a 50-foot-long leash that is connected to a corner of my house. What is the area of the region in which Cassidy can roam? SOMEONE ANSWER

Answer 1

6283.2 ft² (nearest tenth)

Explanation:

The area the goat can roam is the sum of portions of circles.

Draw a diagram to model the situation (see attachment).

The rectangular house is ABCD.

The goat is tethered to corner A on a 50 ft leash. Therefore, the area it can travel if its leash is in a straight line is three-quarters of a circle with radius 50 ft (green on attached diagram).

If the goat travels directly along the side of the house labelled AB to corner B, 30 ft of its leash will be along the side of the house. Therefore, the area it can travel around the corner of B towards C will be a quarter of a circle with radius 20 ft (blue on attached diagram).

Similarly, if the goat travels directly along the side of the house labelled AD to corner D, 40 ft of its leash will be along the side of the house. Therefore, the area it can travel around the corner of D towards C will be a quarter of a circle with radius 10 ft (red on attached diagram).

Area of a circle

`A=\pi r^2`

where r is the radius.

Therefore, the total area of the region in which the goat can roam is:

`\begin{aligned}\implies \textsf{Total area}&=(3)/(4) \pi (50)^2+(1)/(4) \pi (20)^2+(1)/(4) \pi (10)^2\\\\& = (3)/(4) \pi (2500)+(1)/(4) \pi (400)+(1)/(4) \pi (100)\\\\& = (7500)/(4) \pi+(400)/(4) \pi +(100)/(4) \pi\\\\& = 1875\pi+100 \pi +25 \pi\\\\& = 2000 \pi\\\\& = 6283.18530...\\\\& = 6283.2\; \sf ft^2\;(nearest\; tenth)\end{aligned}`