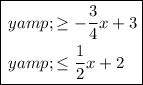Question

Please help for 100 points

Choose the system of inequalities whose solution is the shaded region in the following graph.
1.y ≥ -3/4x + 3
y ≤ 1/2x + 2
2.y ≥ -3/4x + 3
y ≥ 1/2x + 2
3.y ≤ -3/4x + 3
y ≥ 1/2x + 2
4.y ≤ -3/4x + 3
y ≤ 1/2x + 2

Answer 1

`\begin{aligned}\textsf{1.} \quad y & \geq-(3)/(4)x+3\\y & \leq(1)/(2)x+2\end{aligned}`

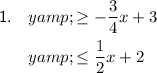
Explanation:

When a line has a positive slope, the y-values increase as the x-values increase.

When a line has a negative slope, the y-values decrease as the x-values increase.

Given equations:

`y=-(3)/(4)x+3 \quad \rightarrow \textsf{negative\;slope}`

`y=(1)/(2)x+2 \quad \rightarrow \textsf{positive\;slope}`

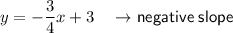
When graphing inequalities:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

Therefore, from inspection of the given graph:

• The line with the negative slope has shading above the line:
  `\implies y\geq-(3)/(4)x+3`
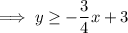
• The line with the positive slope has shading below the line:
  
  `\implies y \leq(1)/(2)x+2`

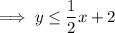
Therefore, the system of inequalities that represents the given graph is:

`\boxed{\begin{aligned} y & \geq-(3)/(4)x+3\\y & \leq(1)/(2)x+2\end{aligned}}`