Question

Find the perimeter and area of a triangle with a base of 9 cm, height of 9.3 cm, and sides of 12

cm and 19 cm. Round to the nearest hundredth when necessary.

Answer 1

The perimeter of the triangle is 40 cm, and the area is 41.85 cm².

Step-by-step explanation:

The perimeter of a triangle is the sum of the lengths of its sides. In this case, the triangle has sides of 9 cm, 12 cm, and 19 cm. Therefore, the perimeter would be:

Perimeter = 9 cm + 12 cm + 19 cm = 40 cm.

The area of a triangle is given by the formula 1/2 × base × height. With a base of 9 cm and a height of 9.3 cm, the area would be:

Area = 1/2 × 9 cm × 9.3 cm = 41.85 cm².

Answer 2

P(perimeter) = 40 cm A(area) = 41.85 ≈ 41.9 cm

Step-by-step explanation:

To find the perimeter of any shape, you just add the length of the sides together. Therefore, you would add the base, 9 cm, with the sides, 12 and 19 cm. 9 + 12 = 21 + 19 = 40 cm, so the perimeter is 40 cm.

To find the area, you need to use the formula for the area of triangles, which is
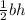`(1)/(2) bh`, where b = base and h = height. So, you would plug the numbers in to get
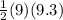`(1)/(2) (9)(9.3)`. This equals
`(1)/(2) (83.7)`, which equals 41.85 cm. Since the question says to round to the nearest hundredth, the final answer would be 41.85 ≈ 41.9 cm.