Question

How can proportional relaships help solve problems

Answer 1

tldr: we can set up constant proportions:
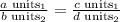`\frac{a \text{ units}_1}{b \text{ units}_2} = \frac{c\text{ units}_1}{d\text{ units}_2}` to solve for values.

Explanation:

Proportional Relationships can help in certain situations where values scale proportionally.

For example let's say I take 10 minutes to do 3 pages of work.

I can solve for how long it takes me to do each page:
`\frac{3\text{ pages}}{10 \text{ minutes}}`

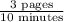
Now in real life this isn't going to be constant, because after a certain amount of time humans get tired, and to be this consistent across many minutes is very unrealistic.

But assuming humans don't get tired and it's completely consistent, we can assume this proportion of:
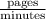`\frac{\text{pages}}{\text{minutes}}` should be constant, which it represents the amount of pages we do per minute.

This is useful because know this value is equal to
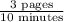`\frac{3\text{ pages}}{10 \text{ minutes}}` in one scenario, I know this is equal in all scenarios.

So I can set up a proportion as such:
`\frac{3\text{ pages}}{10 \text{ minutes}} = \frac{x \text{ pages}}{y \text{ minutes}}`

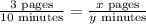
to solve for how many pages I can do in "y" minutes, or how many minutes it takes to do "x" pages.