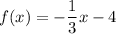Question

Help me pleaseee!!!





thank you

Answer 1

`f(x) = -(1)/(3)x - 4`

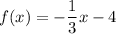
Explanation:

First, find the slope of the line (m) using the equation

`m=(y_2 - y_1)/(x_2 - x_1)`

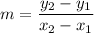
FOR (-6, -2) and (-9, -1):

`x_1 = -6`,
`y_1 = -2`

`x_2 = -9`,
`y_2 = -1`

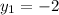
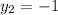
When plugging these values into the slope equation, we get:

`m = (-1 - (-2))/(-9-(-6)) = (1)/(-3) = -(1)/(3)`

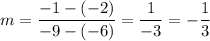
So, the slope of the line is -1/3.

Next, plug the slope value along with one of the given points on the line into the point-slope equation with point (a, b):

`y - a = m(x - b)`

`y - (-2) = -(1)/(3)(x - (-6))`

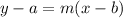
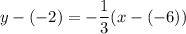
and simplify.

`y + 2 = -(1)/(3)(x + 6)`

`y + 2 = -(1)/(3)x - 2`

`y = -(1)/(3)x - 2 - 2`

`y = -(1)/(3)x - 4`

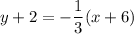
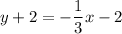
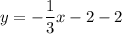
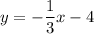
Finally, replace y with f(x) to get:

`f(x) = -(1)/(3)x - 4`