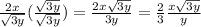Answer:

Explanation:
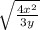 , by laws of roots,
, by laws of roots,
 , so
, so
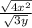 , and by laws of roots,
, and by laws of roots,
 , therefore
, therefore
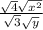 , since only the numerator simplifies into real numbers, keep the
, since only the numerator simplifies into real numbers, keep the
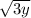 , or,
, or,
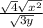 , then
, then
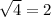 and
and
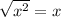 , therefore,
, therefore,
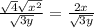 . Then in order to rationalize the denominator, multiply both the numerator and denominator by the denominator, or,
. Then in order to rationalize the denominator, multiply both the numerator and denominator by the denominator, or,
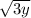 , therefore,
, therefore,