Question

Identify the domain of the expression ((6x^(2)-13x-5))/(x+7)

Answer 1

`(-\infty,-7)\cup(-7,\infty)`

Explanation:

The domain of a function, f, is the set of valid inputs for that function or, where it is not undefined or indeterminate.

`f(x)=(6x^2-13x-5)/(x+7)`

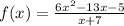
In order to find an undefined value of a rational function, set the denominator equal to 0,
`x+7=0 \Rightarrow x=-7`

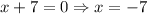
In order to verify that this value is undefined and not indeterminate, plug it into the numerator, and if it does not equal zero, f is undefined at that point.
`6(-7)^2-13(-7)-5=380\\eq0`

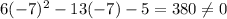
This means that f is discontinuous, or, undefined at
`x=-7`

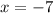
Which makes the domain of the function, f, as
`(-\infty,-7)\cup(-7,\infty)`