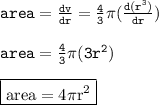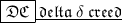Question

Derive the formular to find the area of the moon and state the assumption taken clearly, physically and mathematically, without defying Keplars laws​

Answer 1

Area = 4πr²

Explanation:

- We know that a moon revolves around its orbit as per Keplar. The moon is not a perfect sphere, so we shall take an assumption;

Assume the moon is a perfect and regular sphere

`{ \tt{volume \: of \: moon = (4)/(3) \pi {r}^(3) }} \\ \\ { \boxed{ \tt{ \: v = (4)/(3) \pi {r}^(3) }}}`

- From engineering mathematics (rates of change), we know that volume is first order integral of area and area is the first order derivative of volume;

`{ \tt{area = (d(volume))/(dr) }} \\ \\ { \tt{volume = \int area \: dr}}`

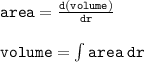
- So, from our formular;

`{ \tt{area = (dv)/(dr) = (4)/(3)\pi ( \frac{d ({r}^(3) )}{dr} ) }} \\ \\ { \tt{area = (4)/(3)\pi(3 {r}^(2)) }} \\ \\ { \boxed{ \rm{area = 4\pi {r}^(2) }}}`

• r is radius of the moon

`{ \boxed{ \mathfrak{DC}}}{ \underline{ \mathfrak{ \: delta \: \delta \: creed}}} \\`