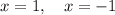Answer:
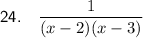
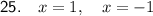
Explanation:
Question 24
Given expression:

When adding rationals with different denominators, make the denominators the same by finding the least common denominator.
Create a common denominator by:
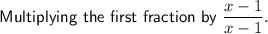

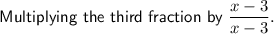
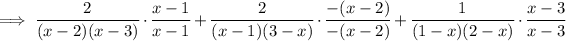
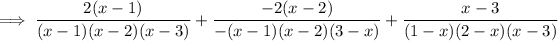
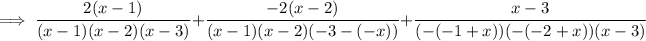
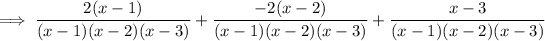
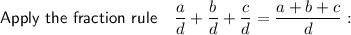
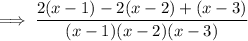
Expand the numerator:
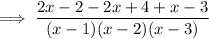
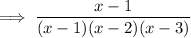
Cancel the common factor (x - 1):
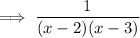
Question 25
Given equation:
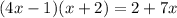
Expand the left side:
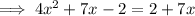
Subtract 7x from both sides:


Add 2 to both sides:
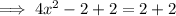

Divide both sides by 4:
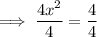
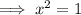
Square root both sides:
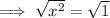
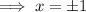
Therefore, the solutions are: