Answer:
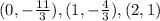
Explanation:
Given Equation:
Required:
- Solve the equation for
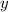 .
. - Find ordered pairs.
Steps:
Subtract 7x from both sides of the equation.
-3y = 11 - 7x
Divide each term in -3y = 11 - 7x by -3 and simplify.
-3y/-3 = 11/-3 + -7x/-3
Simplify the left side.
Cancel the common factor of -3.
-3y/-3 (canceled) = 11/-3 + -7x/-3
Divide y by 1.
y = 11/-3 + -7x/-3
Simplify the right side.
Simplify each term.
Move the negative in front of the fraction.
y = -11/3 + -7x/-3
Dividing two negative values results in a positive value.
y = -11/3 + 7x/3
Choose any value for x that is in the domain to plug in to the equation.
Choose 0 to substitute in for x to find the ordered pair.
Remove parentheses.
y = -11/3 + 7(0)/3
Simplify -11/3 + 7(0)/3.
⇒ Combine the numerators over the common denominator.
y = -11/3 + 7(0) / 3
Simplify the expression.
y = -11 + 0/3
y = -11/3
- Move the negative in front of the fraction.
y = -11/3
Use the x and y values to form the ordered pair.
(0, -11/3)
Choose 1 to substitute in for x to find the ordered pair.
Remove parentheses.
y = -11/3 + 7(1)/3
Simplify -11/3 + 7(1)/3.
Combine the numerators over the common denominator.
y = -11/3 + 7(1)/3
Simplify the expression.
Multiply 7 by 1.
y = -11 + 7/3
Add -11 and 7.
y = -4/3
Move the negative in front of the fraction.
y = -4/3
Use the x and y values to form the ordered pair.
(1, -4/3)
Choose 2 to substitute in for the x in the ordered pair.
Remove parentheses.
y = -11/3 + 7(2)/3
Simplify -11/3 + 7(2)/3.
Combine the numerators over the common denominator.
y = -11/3 + 7(2)/3
Simplify the expression.
Multiply 7 by 2.
y = -11 + 14/3
Add -11 and 14.
y = 3/3
Divide 3 by 3,
y = 1
Use the x and y values to form the ordered pair.
(2, 1)
These are three possible solutions to the equation.
(0, -11/3), (1, -4/3), and (2,1)
Thanks,
Eddie