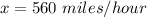Question

Two planes left the same airport traveling in opposite directions. The

lirections. The first plane left at 9:00 a.m. and 2.25 hours later, the two planes
were 1825 miles apart. The second plane left at 10:00 a.m. and its average
average rate. Let x represent the first plane's average rate.
rate was 108 miles per hour slower than the first plane's
What was the first plane's average rate?
Enter an equation that can be used to solve this problem in the first box.
Solve for x and enter the first plane's average rate in the second box.

Answer 1

Answer: x=560 miles per hour

Explanation:

`\displaystyle\\2.25=\\\\2(1)/(4)= \\\\(2*4+1)/(4)=\\\\(8+1)/(4)=\\\\(9)/(4)\ hours`

The second plane left at 10:00 a.m. so, him fly was 1.25 hours:

`\displaystyle\\1.25=\\\\1(1)/(4)=\\\\(1*4+1)/(4)=\\\\(4+1)/(4) =\\\\(5)/(4) \ hours`

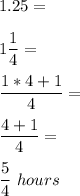
Let x represent the first plane's average rate

Hence, (x-108) represent the second plane's average rate

So,

`\displaystyle\\(9)/(4)x+(5)/(4) (x-108)=1825\ \ \ \ (1)\\`

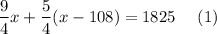
Multiply both parts of the equation by 4:

`9x+5(x-108)=7300\\\\9x+5x-540=7300\\\\14x-540+540=7300+540\\\\14x=7840`

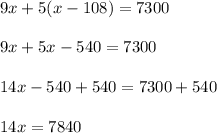
Divide both parts of the equation by 14:

`x=560\ miles/hour`