Question

. If a is a solution of |x + 3| < 8, then a is also a

solution of x + 3 > -8. True or false. Please explain why if it’s false

Answer 1

True

Explanation:

You want to know if it is true that a solution of |x+3|<8 is necessarily a solution of x+3>-8.

Absolute value

The absolute value function is a piecewise linear function that can be described by ...

`|x|=\begin{cases}x&x\ge0\\-x&x < 0\end{cases}`

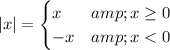
Application

This means the given equation can be interpreted as ...

`\begin{cases}x+3 < 8&(x+3)\ge0\\-(x+3) < 8&(x+3) < 0\end{cases}`

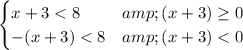
The first inequality has solution ...

x < 5 . . . . . . subtract 3; equivalent for x ≥ -3

The second inequality is the same as ...

x +3 > -8 . . . . . . multiply by -1; equivalent for x < -3

and has solution

x > -11 . . . . . . . . for x < -3

That is, the solution space of the original absolute value inequality is ...

{-11 < x < -3} ∪ {-3 ≤ x < 5} ≡ {-11 < x < 5}

Any member of this set will also be a member of the set that is the solution to x+3 > -8, which is {-11 < x}.

It is true that any solution to |x+3| < 8 is also a solution to x+3 > -8.

__

Additional comment

The above essentially tells us that the inequality |f(x)| < a will resolve to the compound inequality ...

-a < f(x) < a