Answer:
40 cm
Explanation:
Pythagoras Theorem
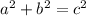
where:
- a and b are the legs of the right triangle.
- c is the hypotenuse of the right triangle.
Let a be the shorter leg.
If the hypotenuse is 1 cm longer than twice the shorter side then:
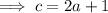
If the hypotenuse is 2 cm longer than the other side then:
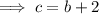
Equate the two expressions for c and solve for b:
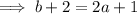
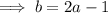
Substitute the expression for c involving a, and the expression for b involving a, into Pythagoras Theorem and solve for a:
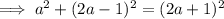
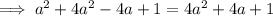
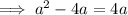
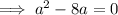
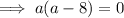
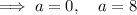
Since the length of a side cannot be zero, a = 8.
The perimeter of a two-dimensional shape is the distance around the outside. Therefore, the perimeter of the triangle is the sum of its sides:
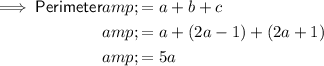
Substitute the found value of a into the expression for the perimeter:
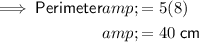
Therefore, the perimeter of the triangle is 40 cm.