Answer:
(a) FB = 24 cm
(b) r = 10
Explanation:
Part (a)
Find the length, in cm, of FB.
Intersecting Secant and Tangent Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Given:
- Tangent segment = FB
- Secant segment = FE = 18 + 14 = 32 cm
- External secant segment = FD = 18 cm
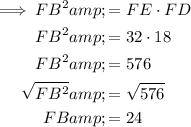
Therefore, the length of FB is 24 cm.
Part (b)
Find the value of r.
Triangle FBO is a right triangle with side lengths:
- BO = r cm
- FB = 24 cm
- OF = (r + 16) cm
Pythagoras Theorem

where:
- a and b are the legs of the right triangle.
- c is the hypotenuse (longest side) of the right triangle.
Therefore, substitute the side lengths of triangle FBO into Pythagoras Theorem and solve for r:

Therefore, the value of r is 10.