Should be B.
There is a nested function structure. Let's first look at the limit of the interior (f(0)). The point we need to pay attention here is to look at the limits from the right and left. If both values are equal, we can say that it has a limit at that point.
If we express it algebraically;
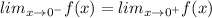 then,
then,
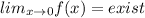
The left limit and the right limit of
 are equal and equal to
are equal and equal to
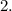
The left limit and the right limit of f(2) are equal and equal to 3.
As I have drawn with colored arrows in the graph below, we approach from the left and from the right, and if they both point to the same point, we can talk about the existence of the limit at that point. Otherwise, this function does not have a limit at that point.