Question

Consider the sequence of positive integers defined by a_{n+1} = na_nan+1​=nan​ for integers n≥1n≥1. If a_1≤1000a1​≤1000, find the sum of all the possible number of zeroes a_{2022}a2022​ can end with.​

Answer 1

By substitution,

`a_(n+1) = na_n \\ a_(n+1) = n(n-1) a_(n-1) \\ a_(n+1) = n(n-1)(n-2)a_(n-2) \\ ~~~~~~~~~ \vdots \\ a_(n+1) = n(n-1)(n-2)\cdots(n-k)a_(n-k)`

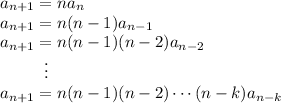
so that after
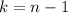`k=n-1` steps, we end up with

`a_(n+1) = n(n-1)(n-2)\cdots(n-(n-1)) a_(n-(n-1)) = n! a_1 \\\\ ~~~~ \implies a_(2022) = 2022! a_1`

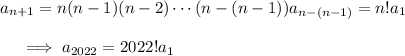
A trailing zero in 2022! comes from factor of 10 = 2×5. The prime factorization of 2022! has a lot more 2s than 5s, so we only need to count how many 5s occur in the factorization. Note that

2022 = 5×404 + 2 ⇒ 404 multiples of 5

2022 = 5²×80 + 22 ⇒ 80 multiples of 5²

2022 = 5³×16 + 22 ⇒ 16 multiples of 5³

2022 = 5⁴×3 + 147 ⇒ 3 multiples of 5⁴

and 5⁵ = 3125 > 2022. So there is total of

404 + 80 + 16 + 3 = 503

distinct factors of 5 in 2022!, and thus 503 trailing zeros in 2022!.

Since
`1\le a_1\le1000`, and the highest power of 5 that divides 1000 is 5⁴ = 625, we know that multiplying 2022! by
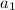`a_1` can introduce up to 4 more pair-able factors of 5.

So the sum of all the possible numbers of zeros in
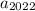`a_(2022)` is

503 + 504 + 505 + 506 + 507 = 2525