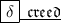Answer:
Area is 314.2 cm²
Explanation:
- Consider a circle whose radius is r, while calculating its area, the formula is derived from its circumference;
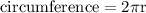
- but area is the integral of circumference;
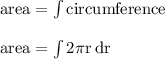
- Assume area is between the center to the edge from r = 0 to r = r
![{ \rm{area = 2\int^(r)_(0)\pi r \: dr}} \\ \\ { \rm{area = 2[\pi ( \frac{ {r}^(2) }{2} )]^(r) _(0) }} \\ \\ { \rm{area = \pi {(r)}^(2) - \pi {(0)}^(2) }} \\ \\ { \boxed{ \rm{area = \pi {r}^(2) }}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/77v7z3w2appkxjunzgysq9ozvqq3kcsdtk.png)
- From the question given, the circle has a radius of 10cm