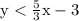Question

Which inequality is represented by the graph?

Answer 1

`y < (5)/(3) x - 3 \\`

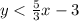
Explanation:

- General linear equation of a line passing through point (x, y) with a gradient m and y-intercept (0, c) is ;

`{ \rm{y = mx + c}}`

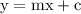
- As finding gradient, m; consider points (0, -3) and (3, 2) from the graph;

`{ \rm{slope \: m = (2 - ( - 3))/(3 - 0) }} \\ \\ { \rm{m = (5)/(3) }}`

- Then our equation becomes y = 5/3x + c

- Consider point (0, -3), relate it with (0, c) hence c is -3;

`{ \rm{y = (5)/(3)x - 3 }}`

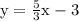
- If you see the format of the coordinates, x coordinates are greater than y coordinates, hence y < x

`{ \rm{y < (5)/(3)x - 3 }} \\`

Answer 2

`y < (5)/(3)x-3`

Explanation:

All given answer options have the same linear equation:

`y=(5)/(3)x-3`

Therefore, there is no need to work out the equation of the line for this question as it is already given.

When graphing inequalities:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

From inspection of the graph there is:

• A dashed line.
• Shading under the line.

Therefore, the inequality that is represented by the graph is:

`y < (5)/(3)x-3`