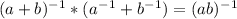Question

Prove that:
`(a+b)^(-1) . (a^(-1) + b^(-1) ) = (ab)^(-1)`

Answer 1

Explanation:

`(1)/(a + b) * ( (a + b)/(ab)) = (1)/(ab)`

Answer 2

Answer with step-by-step explanation:

`(a+b)^-^1*(a^-^1+b^-^1)=(ab)^-^1`

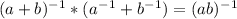
First, convert these into positive indices.

`(1)/((a+b)) *((1)/(a) +(1)/(b))=(1)/(ab)`

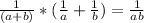
And now, let us solve the left side.

`(1)/((a+b)) *((1)/(a) +(1)/(b))\\\\`

First, solve the brackets. That is add the fractions inside the brackets.

`(1)/((a+b)) *((1)/(a) +(1)/(b))\\\\(1)/((a+b))*((1*b)/(a*b) +(1*a)/(b*a))\\\\(1)/((a+b))*((b)/(ab) +(a)/(ab))\\\\(1)/((a+b))*((a+b))/(ab)`

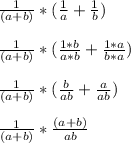
Now multiply the fractions.

`(1)/(ab)`

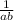
So, it's clear that the left side equals the right side.

Left side = Right side

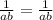
`(1)/(ab)=(1)/(ab)`

∴
`(a+b)^-^1*(a^-^1+b^-^1)=(ab)^-^1`