Answer:
3 seconds
Explanation:
The height of the rocket when it hits the ground will be zero meters.
Therefore, set the equation to zero and solve for t by using the quadratic formula.
Quadratic Formula
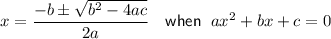
Given equation:
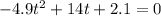
Therefore:
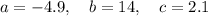
Substitute the values into the quadratic formula:
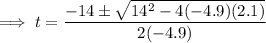
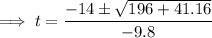
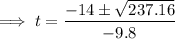
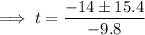
Therefore:
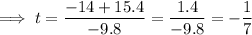
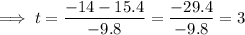
As time is positive, t = 3 s only.
Therefore, it will take 3 seconds for the rocket to hit the ground.