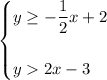Question

50 POINTS

What system of linear inequalities is shown in the graph? Enter your answers in the boxes.

enter your answers in the boxes
□
□​

Answer 1

`\begin{cases}y \geq -(1)/(2)x+2\\\\y > 2x-3\end{cases}`

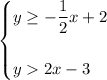
Explanation:

Find the equations of the two lines by substituting two points on each line into the slope formula to find the slope, then substituting the found slope and one of the points into the point-slope formula.

Equation of Line 1

Points on the line: (0, 2) and (2, 1).

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(1-2)/(2-0)=-(1)/(2)`

Substitute the found slope and one of the points into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-2=-(1)/(2)(x-0)`

`\implies y=-(1)/(2)x+2`

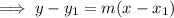
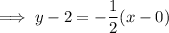
Equation of Line 2

Points on the line: (0, -3) and (2, 1).

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(1-(-3))/(2-0)=-(4)/(2)=2`

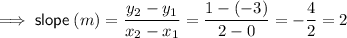
Substitute the found slope and one of the points into the point-slope formula:

`\implies y-y_1=m(x-x_1)`

`\implies y-(-3)=2(x-0)`

`\implies y=2x-3`

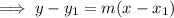
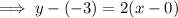
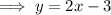
When graphing inequalities:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

As the line for equation 1 is solid and there is shading above the line, the line is represented by the inequality:

`\boxed{y \geq -(1)/(2)x+2}`

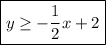
As the line for equation 2 is dashed and there is shading above the line, the line is represented by the inequality:

`\boxed{y > 2x-3}`

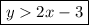
Therefore, the system of linear inequalities shown in the graph is:

`\begin{cases}y \geq -(1)/(2)x+2\\\\y > 2x-3\end{cases}`