Question

8.
S
-80
ZX D
lo
Please help
HELP PLEASE

Answer 1

`\begin{aligned}&\phantom{=.} (1)/(8)x \cdot (-4)/(5)x\\\\&=(1)/(2) \cdot \frac{\boxed{-1}}{5} \cdot x \cdot \boxed{x}\\\\& = \frac{\boxed{-1}}{\boxed{10}} \;x\;^\boxed{2}\end{aligned}`

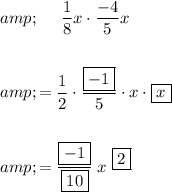
Explanation:

According to the Commutative Property Law of Multiplication, changing the order or position of the numbers does not change the end result.

Therefore, collect like terms by moving the fractions to the left and the variables to the right.

As the denominator of the first fraction has been divided by 4, the numerator of the second fraction should also be divided by 4.

Therefore:

`=(1)/(2) \cdot \frac{\boxed{-1}}{5} \cdot x \cdot \boxed{x}\\`

`\textsf{Apply\;the\;fraction\;rule} \quad (a)/(c)\cdot (b)/(d)=(ab)/(cd).`

`\textsf{Apply\;the\;exponent\;rule}\quad \:aa=a^2.`

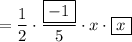
Therefore:

`=\frac{\boxed{-1}}{\boxed{10}} \;x\;\boxed{^2}`