Answer:

Explanation:
The picture itself measures 6" by 8". Therefore, the area is 6 * 8 = 48 square inches.
All of the pieces of wood have the same width, and we know that two of them will be 6 inches long and two will be 8 inches long.
Therefore, the combined area of the pieces of wood will be 2 * 6w and 2 * 8w. This gives us 12w + 16w.
Now we can set up an inequality:
48 (area of picture) + 12w + 16w <= 100 (maximum area).
Simplify the left side of the equation to give us this:
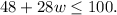
We can move the 48 over to the other side to get
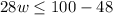 , which simplifies to
, which simplifies to
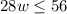 . Now, you just have to divide both sides by 28 to get
. Now, you just have to divide both sides by 28 to get
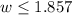 .
.
Rounding to the nearest tenth of an inch gives us 1.9 as the maximum width of the pieces of wood.