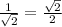Question

Given the diagram below, what is COS(45º)?

Answer 1

1 /
`√(2)`

Step-by-step explanation:

In a 45,45,90 triangle, the two legs of the triangle are equal to each other and the hypotonus being x
`√(2)`. So that make the unknown sides 6 and 6
`√(2)`. When solving for cos(45) you divide the leg adjacent to the 45 (6) by the hypotonus (6
`√(2)`) This gives you 6/6
`√(2)`. You can simplify the 6s to get 1 /
`√(2)`

Answer 2

Answer: Choice C

Step-by-step explanation:

This is a 45-45-90 right triangle, aka isosceles right triangle.

The two legs are 6 units each, because the legs of isosceles triangles are the same length.

The hypotenuse is 6*sqrt(2) through the use of the pythagorean theorem.

From here we can say:

`\cos\left(\text{angle}\right) = \frac{\text{adjacent}}{\text{hypotenuse}}\\\\\cos\left(45^(\circ)\right) = (6)/(6√(2))\\\\\cos\left(45^(\circ)\right) = (1)/(√(2))\\\\`

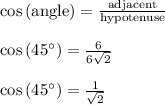
It turns out that the '6' has nothing to do with the final answer, since the '6's cancel out. So we could change that 6 to any number we want, and the answer would still be the same.

Side note: Rationalizing the denominator will have
`(1)/(√(2)) = (√(2))/(2)`