Question

Solve the equation.

x^2 + 7x = 0

Answer 1

`\quad \huge \quad \quad \boxed{ \tt \:Answer }`

`\qquad \tt \rightarrow \:x = 0\:\; or \:\: x = -7`

____________________________________

`\large \tt Solution \: :`

`\qquad\displaystyle \tt \rightarrow \: {x}^(2) + 7x = 0`

`\qquad\displaystyle \tt \rightarrow \: {x}(x + 7) = 0`

There are two cases now,

Case 1 :

`\qquad\displaystyle \tt \rightarrow \: x = 0`

Case 2 :

`\qquad\displaystyle \tt \rightarrow \: x + 7 = 0`

`\qquad\displaystyle \tt \rightarrow \: x = - 7`

So, the possible values of x are :

`\qquad\displaystyle \tt \rightarrow \: 0 \: \: and \: \: - 7`

Answered by : ❝ AǫᴜᴀWɪᴢ ❞

Answer 2

`x=0, \quad x=-7`

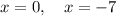
Explanation:

Given equation:

`x^2+7x=0`

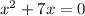
Factor x from the left side of the equation:

`\implies x(x+7)=0`

Using the Zero Product Property, set each factor equal to zero and solve for x:

`\implies x=0`

`\implies x+7=0 \implies x=-7`

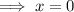
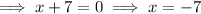
Therefore, the solutions of the equation are:

`x=0, \quad x=-7`

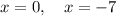
Zero Product Property: If a⋅b = 0 then either a = 0 or b = 0 (or both).