Answer:

Explanation:
By definition of a negative exponent:
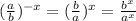
In the last step I simply distributed the exponent, but this actually goes both ways! So we can do:
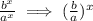
The next thing you need to know is that:
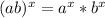
and like the previous statement, it works both ways! So this means:
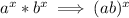
So the denominator of the expression given can be expressed as:

Lastly you need to understand:
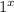 just simplifies to one, because
just simplifies to one, because
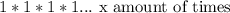 will stay equal to one. So we can thing of 1 as being raised to some number, even if not explicitly stated.
will stay equal to one. So we can thing of 1 as being raised to some number, even if not explicitly stated.
This helps because we can write one as:
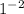
so now we have the expression:
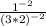
Well this can because now we can "factor" out this exponent just like how it was demonstrated in the beginning
We get the expression:
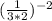
Now we use the definition of a negative exponent, to get the reciprocal giving us the expression
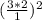
We can now "distribute" this exponent across the division to get
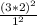
Well 1 squared just simplifies to 1, so it's redundant to write.
This gives us the expression:
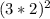
and as stated before we can distribute this across multiplication, and another way to think of it is:
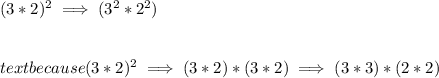
we're just grouping the like terms, so we can write them as an exponent.
So this gives us our final expression:

or

which is the option B, since the order in which we multiply does not matter.