Answer:
A.
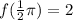
B.
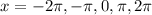
C.
![[-2, 2]](https://img.qammunity.org/2023/formulas/mathematics/college/z0n3axcgyvh33lr1mwkkynldbaotzkhz71.png)
Explanation:
A:
Since we want to find:
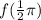 , all we do is go that that x-value on the function and then go either up or down until we find where the y-value is at that x-value, because
, all we do is go that that x-value on the function and then go either up or down until we find where the y-value is at that x-value, because
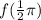 is just another way of expressing "the y-value of the function f, at
is just another way of expressing "the y-value of the function f, at
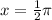
In this case it turns out that the y-value is two, which you can verify by going to that x-value and finding where the y-value is at that point.
So:
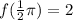
B.
To find all the x-values such that:
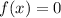 , we just need to find where the graph crosses the x-axis, also known as an x-intercept. This is because at an x-intercept, the y-value will be equal to zero.
, we just need to find where the graph crosses the x-axis, also known as an x-intercept. This is because at an x-intercept, the y-value will be equal to zero.
Looking at the graph you can see that these x-intercepts occur at:
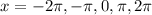
in general you'll notice that all the values are actually separated by a value of pi, so the general formula for a zero in this equation is likely going to be:
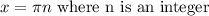 , since trigonometric functions are periodic, they repeat.
, since trigonometric functions are periodic, they repeat.
C.
Looking at the graph you'll notice the value is increasing, then decreasing, then increasing... and so on.
The max value it reaches is two, and the min value it reaches is negative two.
The range of a function is the y-values that the function can output, considering all the possible inputs, or the domain.
In this case no matter the input we can only output values between -2 and 2.
In this interval notation, we use brackets, since the minimum and maximum possible values are included in the range, since the function does output 2 and -2, it doesn't just "approach" it.
So we get a range of:
![[-2, 2]](https://img.qammunity.org/2023/formulas/mathematics/college/z0n3axcgyvh33lr1mwkkynldbaotzkhz71.png)