Answer:
23 and 110
Explanation:
using the expansion
(a + b)² = a² + 2ab + b² , then
a +
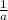 = 5 ( square both sides )
= 5 ( square both sides )
(a +
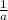 )² = 5²
)² = 5²
a² + 2(a ×
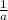 ) +
) +
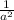 = 25
= 25
a² + 2(1) +
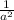 = 25
= 25
a² + 2 +
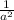 = 25 ( subtract 2 from both sides )
= 25 ( subtract 2 from both sides )
a² +
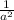 = 23
= 23
---------------------------------------------------------------------
using the expansion
(a + b)³ = a³ + b³ + 3ab(a + b) , then
a +
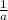 = 5 ( cube both sides )
= 5 ( cube both sides )
(a +
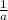 )³ = 5³
)³ = 5³
a³ +
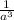 + 3(a ×
+ 3(a ×
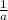 )(a +
)(a +
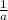 ) = 125
) = 125
a³ +
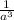 + 3(1)(5) = 125
+ 3(1)(5) = 125
a³ +
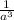 + (3 × 5) = 125
+ (3 × 5) = 125
a³ +
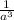 + 15 = 125 ( subtract 15 from both sides )
+ 15 = 125 ( subtract 15 from both sides )
a³ +
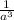 = 110
= 110