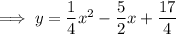Answer:
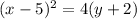
Please note that alternative forms of this equation (vertex and standard) are in the explanation.
Explanation:
Standard form of a parabola with a vertical axis of symmetry:
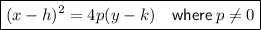
- Vertex = (h, k)
- Focus = (h, k+p)
Given:
- Vertex = (5, -2)
- Focus = (5, -1)
Therefore:
Calculate p:
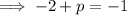
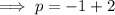
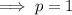
Substitute the values of h, k and p into the formula to create an equation of the parabola with the given parameters:
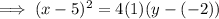
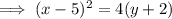
In vertex form:
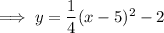
In ax² + bx + c form: