Answer:
31.4 cm
Explanation:

The y-intercept is the y-value when x is zero, so the initial value.
If the initial amount of snow is 72 cm, the y-intercept is 72.
The slope is the rate of change.
If the snow is melting at a rate of 5.8 cm per day, then the rate of change is -5.8.
Therefore, the equation that models the given word problem is:

To find how much snow is left after 7 days, substitute x = 7 into the found equation:
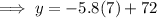
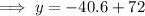
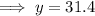
Therefore, there will be 31.4 cm of snow left after seven days of warm weather.