Question

For questions 7 through 9, Albert and friends are stranded in a clearing on top of a hill at an

elevation of 350m above sea level. You are on a rescue plane flying in supplies to tide them over
until help arrives. Your plane is flying at a constant speed of 260 km/h from west to east at an
elevation of 810m.

PLEASE HELP WOTH THESE QUESTIONS!!!!!!

Answer 1

Assume that the air resistance on the supplies is negligible, and that
`g = 9.8 \; {\rm m\cdot s^(-2)}`.

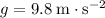The plane need to drop the supplies when it is horizontally approximately
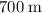`700\; {\rm m}` away from the hill.

The supplies will hit the tree.

Step-by-step explanation:

Let
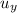`u_(y)` and
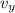`v_(y)` denote the initial and final vertical velocity of the supply;
`u_(y) = 0\; {\rm m\cdot s^(-1)}` since the plane was flying horizontally.

Let
`x_(y)` denote the vertical displacement of the supply;
`x_(y) = 350\; {\rm m} - 810\; {\rm m} = (-460)\; {\rm m}`.

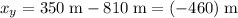Let
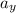`a_(y)` denote the vertical acceleration of the supply;
`a = (-g) = (-9.8)\; {\rm m\cdot s^(-2)}`.

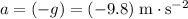Make use of the SUVAT equation
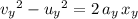`{v_(y)}^(2) - {u_(y)}^(2) = 2\, a_(y)\, x_(y)` to find
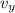`v_(y)`, the final vertical velocity of the supply:

`\begin{aligned} {v_(y)}^(2) &= {u_(y)}^(2) + 2\, a_(y)\, x_(y) \end{aligned}`.

`\begin{aligned} v_(y) &= -\sqrt{{u_(y)}^(2) + 2\, a_(y)\, x_(y)} \\ &= -\sqrt{0^(2) + 2\, (-9.8)\, (-460)}\; {\rm m\cdot s^(-1)} \\ &\approx (-94.953)\; {\rm m\cdot s^(-1)} \end{aligned}`.

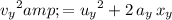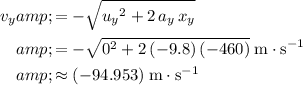(Negative since the supply would be travelling downwards.)

Let
`t` denote time it takes for the supply to land on the hill after being dropped from the plane. Make use of the SUVAT equation
`t = (v_(y) - u_(y)) / (a)` to find the value of
`t\!`:

`\begin{aligned} t &= (v_(y) - u_(y))/(a) \\ &\approx ((-94.953) - 0)/((-9.8)) \; {\rm s}\\ &\approx 9.6890 \; {\rm s} \end{aligned}`.

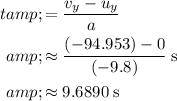Apply unit conversion and ensure that
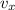`v_(x)`, the horizontal speed of the plane is in the standard unit
`{\rm m\cdot s^(-1)}`:

`\begin{aligned} v_(x) &= \frac{260\; {\rm km}}{1\; {\rm h}} * \frac{1\; {\rm h}}{3600\; {\rm s}} * \frac{1000\; {\rm m}}{1\; {\rm km}} \\ &\approx 72.222\; {\rm m\cdot s^(-1)}\end{aligned}`.

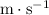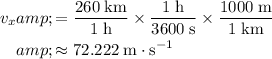Under the assumptions, the horizontal speed of the supply will be the same as that of the plane-
`v_(x) \approx 72.222\; {\rm m\cdot s^(-1)}`- until it lands.

While in the air, the supply will travel a horizontal distance of:

`\begin{aligned}x_(x) &= v_(x)\, t \\ &\approx 72.222\; {\rm m\cdot s^(-1)} * 9.6890\; {\rm s} \\ &\approx 699.76\; {\rm m}\end{aligned}`.

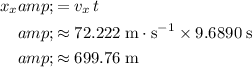Hence, for the supply to land exactly at the top of the hill, the plane need to drop the supply while at a horizontal distance of approximately
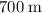`700\; {\rm m}` away from the hill.

The horizontal distance between the trees and the location where the plane dropped the supply would be approximately
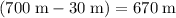`(700\; {\rm m} - 30\; {\rm m}) = 670\; {\rm m}`. The time required for the the supply to reach that horizontal position would be:

`\begin{aligned} t &= (x_(x))/(v_(x)) \approx \frac{669.76\; {\rm m}}{72.222\; {\rm m\cdot s^(-1)}} \approx 9.2736\; {\rm s}\end{aligned}`.

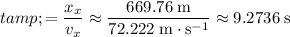Let
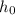`h_(0)` denote the initial height of the supply (relative to the sea level.) In this question,
`h_(0) = 810\; {\rm m}`.

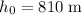Let
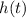`h(t)` denote the height of the supply (relative to the sea level) after being dropped from the plane for time
`t`.

The SUVAT equation
`h(t) = (1/2)\, a\, t^(2) + u_(y)\, t + h_(0)` gives an expression for
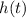`h(t)`. Make use of this equation to find the height of the supply (relative to the sea level) when the supply reach the horizontal position of the trees at
`t \approx 9.2736\; {\rm s}`:

`\begin{aligned} h(t) &= (1)/(2)\, a\, t^(2) + u_(y)\, t + h_(0) \\ &= (1)/(2)* (-9.8)\, (9.2736)^(2) + 0* 9.2736 + 810 \\ &\approx 388.60\; {\rm m} \end{aligned}`.

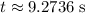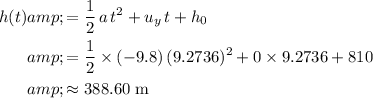Note that the altitude of the top of the trees is
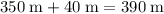`350\; {\rm m} + 40\; {\rm m} = 390\; {\rm m}` relative to the sea level. Since
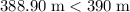`388.90\; {\rm m} < 390\; {\rm m}`, the supplies will run into the trees.